규칙과 대응은 함수 개념의 기초가 되는 중요한 아이디어입니다. 6학년의 정비례, 반비례를 공부하기 전에, 5학년에서는 학생에게 친숙한 일상생활과 주변 현상에서 대응 관계를 탐구할 수 있도록 구성되어 있습니다. 두 양의 대응 관계가 곱셈식, 덧셈식, 뺄셈식, 나눗셈 식 중 하나로 간단하게 나타나는 경우만 다루는 것입니다.
1. 선행학습과 5학년 3단원의 초점
5학년 학생들은 이미 4학년 1학기 때, 수 배열과 계산식의 배열을 중심으로 한 양의 규칙적인 변화를 파악하였습니다. 또 도형이나 변화하는 모양에서도 규칙을 찾은 바 있습니다. 수, 모양뿐 아니라 계산식의 규칙과 관련된 문제 또한 4학년의 6단원 '규칙 찾기' 단원에서 배운 바가 있습니다. 이 단원에서는 학생들이 두 양 사이의 대응 관계를 탐구하고, 이를 '기호'를 이용해 표현하도록 하는데 초점이 있습니다.
2. 한국 현행 수학 교과서의 '대응 관계' 배우기에서 아쉬운 점
첫째, 대응 관계에 대한 명확한 정의가 부족합니다. 쉽게 말하면 서로 짝짓는 것을 대응이라고 합니다. 이거 아니면 다른 짝이 없는 경우이죠. 중학교에 올라가면 물론 일대일 대응, 일대다 대응으로 함수 관계가 다변화되기는 하지만, 초등 단계에서는 주어진 관계에 의하여 서로 짝이 된다는 말을 더 강조해서 알려줄 필요가 있습니다. 학생들은 4학년에서 규칙성을 찾는 것에 대해서는 배웠지만, 대응 관계에 대해서는 본 학년에서 처음 알게 됩니다. 따라서 저는 다음과 같이 한자어, '짝이 되는 관계'와 같은 설명을 보충하여 대응 관계에 대한 초점을 더 맞추었습니다.

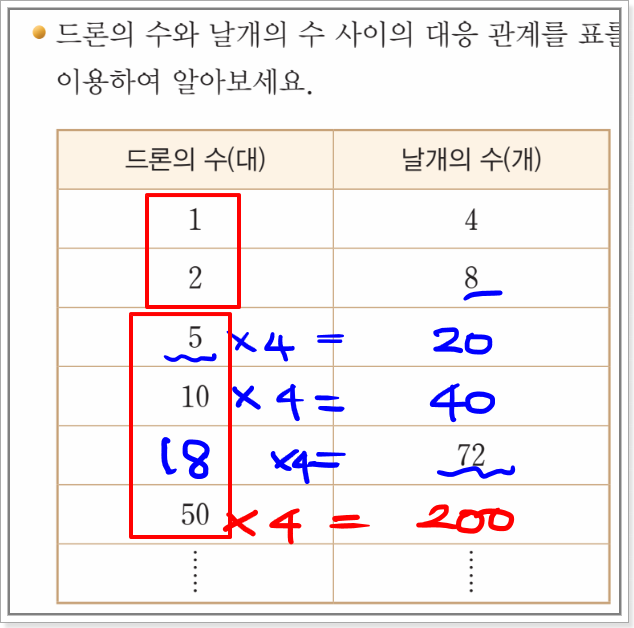
둘째, 대응 관계를 표로 나타내는 연습을 더 했으면 좋겠습니다. 두 수 사이의 대응 관계를 표로 나타내게 되면, 서로 어떤 대응 관계가 있는지 쉽게 알 수 있습니다. 여기에서 더 연습을 하면, 식으로 나타내는 것도 더 쉽게 할 수 있겠죠. 그런데 교과서 54p를 봅시다. 드론의 수가 1, 2... 이렇게 가다가 갑자기, 5, 10, 18, 50의 순서대로 갑자기 숫자가 확 커집니다. 지면을 어느 정도 할애하더라도, 표로 대응관계를 나타내는 연습을 더 해야 하지 않을까 하는 생각이 듭니다.
3. 한국 현행 수학 교과서의 제재 선택에서 아쉬운 점
아이들이 친근하게 여기고, 흥미를 느낄 수 있는 드론을 제재로 선택한 점은 참 바람직합니다. 실제 수업에서 아이들은 드론 이야기에 흥미를 느꼈습니다. 그러나 이어지는 내용에서 곧 절망하고 맙니다..... 시간과 거리 개념이라니요...ㅠㅠ 물론 5학년 과학에서 다루기는 하는 내용입니다. 그런데, 2학기에 나옵니다. 인형에 붙은 단추의 개수, 개구리의 팔의 개수 등 더 쉬운 제재들이 더 많습니다. 굳이 거리=시간 x속력을 연상시키는 이런 질문이 필요한지 궁금합니다.

거리와 시간 관련한 문제는 여기에서만 나오는 것이 아니었습니다. 이어지는 문제에서도 지하철의 이동거리를 묻는 질문이 나옵니다... 학생들은 수업 중에 서로 대응하는 두 '양'이 무엇이냐고 질문하기도 합니다. 'sheep'이 아니라 'amount'라는 개념도 제대로 서지 못한 아이들에게 이런 복잡한 내용은 어려울 수밖에 없습니다.

그래서 전 개인적으로 수학 3단원의 제재를 재구성할 필요를 느꼈습니다. 교과서 상에서는 55~56쪽에서 생활 속 대응관계를 찾고, 그전까지는 대응관계를 식으로 나타내는데 초점을 둡니다. 그러나 저는 동기유발을 '사다리 타기' 등의 대응이 될 수밖에 없는 관계들을 일상생활에서 끌어오도록 합니다. 그리고 대응 관계를 표로 여러 번, 몸에 익을 때까지 반복하게 연습을 시킵니다. 이때는 교과서에서 다루는 것처럼 숫자, 기호 등을 카드로 주어 마음대로 배치하는 것도 좋은 방법입니다. 그다음에야 이 관계들을 식으로 이끌고, 기호로 나타낼 수 있기 때문입니다.
'수학교육' 카테고리의 다른 글
| 5학년 수학 약분과 통분의 계열성_약분과 통분의 선행학습 개념_어려움 (0) | 2021.04.19 |
|---|---|
| 한국 초등 5학년 수학책 46쪽_십간십이지로 알아보는 배수, 최소공배수? (0) | 2021.04.13 |
| 초등학교 고학년(4,5,6학년) 1학기 수학익힘책 풀이 링크(feat. 선행학습이 위험한 이유) (0) | 2021.04.11 |
| 5학년 약수와 배수. [도전 수학]?! 멈춰!!! (feat. 뭘 물어보는거야?) (3) | 2021.04.01 |
| 최소공배수 구하는 방법 재미있게 설명하기! (feat. 수학교과서 고민...) (1) | 2021.03.31 |



댓글