기약 분수는 분모와 분자의 공약수가 오로지 1밖에 없는 분수를 말합니다. 분모와 분자를 같은 수로 나누고, 나누다가 더 이상 약분이 안 되는 분수를 기약 분수라고 하지요. 한국 현행 교과서에서는 약분과 기약 분수를 어떻게 안내하고 있는지 함께 살펴보도록 하겠습니다.
1. '간단한 분수' 용어 정리의 필요성
수업 전, 미리 교과서를 훑다 보면, 마음에 걸리는 용어들이 있습니다. 현행 5학년 수학 교과서 70쪽 또한 그랬는데요. 바로 '간단한' 분수라는 말이었습니다. 약분을 위해서 분모와 분자를 공약수로 나누어서 '간단하게' 만든다는 것입니다. 그런데 이게 학생들에게 제대로 와 닿는 말인지에 대해선 의구심이 듭니다. 학생들은 수학적 용어가 아닌 일상적 용어로 간단하다는 표현을 받아들이기 때문입니다. 간단하다는 것은 더 이상 공통된 약수가 없는 기약 분수에 가까워진다는 의미입니다. 다시 말해, 분모와 분자의 숫자가 더 작아져야 간단하다는 것을 알도록 추가 설명이 필요합니다.
- 그럼 자연스럽게 기약 분수가 무엇인지에 대한 궁금증이 생깁니다. 제 짧은 소견으로는 학생들이 '기약 분수가 뭘까?'라는 궁금증을 가지는데서 시작을 해야 한다고 봅니다. [기약 분수-> 약분]의 순서로 가르쳐야 하지 않을까요?

2. 기약 분수의 오개념 방지하기
이때, 간단하다는 것을 숫자가 작다고 설명하다가 자칫, 기약 분수가 가장 '작은'수라는 잘못된 개념을 갖지 않도록 유의해야 합니다. 기약 분수란 어떤 같은 값을 나타내는 여러 분수들 중에서, 분모와 분자의 공약수가 1밖에 없는 분수이기 때문입니다. 형태가 다를 뿐, 같은 값을 갖는다는 것을 강조할 필요가 있습니다.
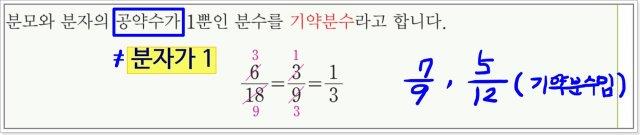
- 실제로 수업 중에 한 학생이 저에게 분자가 1인 것이 기약 분수가 아니냐고 물었습니다.
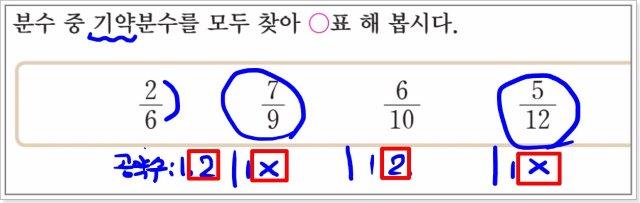
- 공약수가 1이라는 것이지, 분자가 1이라고 생각해서는 안됩니다. 분자가 1이 아니면 기약분수가 아니라고 생각해 버리거든요. 실제로 7/9와, 5/12는 모두 기약분수입니다. 교사는 분모와 분자 간 공약수의 개수가 1개라는 데 초점을 두어야 합니다. 그래서 이 차시의 수업시간에는 기약 분수가 무엇인지 먼저 알기 위해, 분모와 문자의 공약수를 찾아서 밑에 써보는 과정을 거칩니다. 공약수의 개수가 무조건 2개 이상이면, 기약 분수가 될 수 없는 것입니다.
3. 분모와 분자의 최대공약수를 찾으면 기약 분수가 나오는 이유
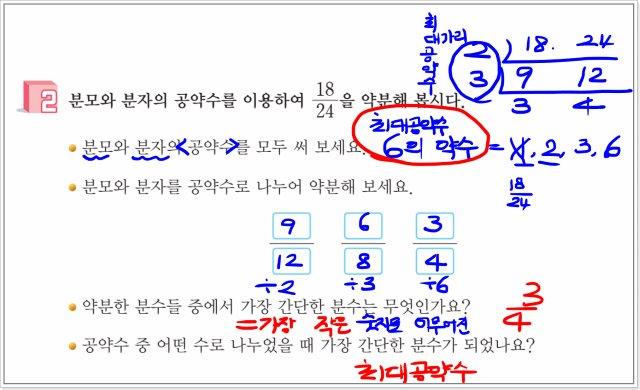
위의 과정에서 학생들이 분모와 분자의 공약수들을 찾다 보면, 기약 분수를 만들기 위해선 공약수 중에 가장 큰 것을 선택해야 함을 알게 됩니다. 한편으로는 학생들이 이미 이전 단원인 2단원, 약수와 배수에서 최대공약수의 약수가 두 수의 공약수임을 알고 있는 상태입니다.
- 따라서 가장 간단한(공약수가 하나밖에 없는) 기약 분수를 만들기 위해서는 두 수의 최대공약수를 아는 것이 편리하다는 결론에 자연스럽게 도달할 수 있습니다.
4. 옳게 말한 친구 좀 그만 찾자... 이유 말하기에 변화 주기
이번 2015 개정 교육과정 수학 교과서에서는 옳게 말한 친구, 옳게 말하지 못한 친구를 엄청 찾습니다. 아무래도 많은 개념들을 한 번에 다룰 수 있어 편리하기는 합니다. 하지만 올바른 것끼리 짝짓기, 수와 설명 연결하기, OX퀴즈 등 다양한 형태의 문제가 있었으면 좋겠다는 아쉬움은 있습니다. 학생들도 이런 문제 형태에 지루함을 느낄 수 있다는 생각이 들었습니다. 그냥 이유만 찾아 말해보라는 답변의 형태도 명료하지 않은 것 같습니다
- 그래서 저는 교과서에다, 이 친구에게 직접 틀린 것을 적으라고 지도합니다. 예를 들어, 약분의 차시이기 때문에 '2로 나눌 것을' 곱했다면, "곱하지 말고 나눠야지!"라고 그 친구에게 말하듯이 직접 적는 것입니다. (이건 약간 유치하다고도 볼 수 있는 간단한 팁이지만... 뭐.... 예..... 나눠봅니다.)

'수학교육' 카테고리의 다른 글
| 한국 5학년 초등 수학, 다각형의 둘레와 넓이 지도시 유의사항(feat.밑변은 밑에 있는 변이 아니야~) (0) | 2021.05.17 |
|---|---|
| 한국 초등 수학 5학년 5단원. 분수의 덧셈과 뺄셈- 잘 지도하는 방법 (0) | 2021.05.10 |
| 5학년 수학 약분과 통분의 계열성_약분과 통분의 선행학습 개념_어려움 (0) | 2021.04.19 |
| 한국 초등 5학년 수학책 46쪽_십간십이지로 알아보는 배수, 최소공배수? (0) | 2021.04.13 |
| 한국 초등 5학년 수학 [3단원-규칙과 대응] 지도하는 법 (0) | 2021.04.13 |



댓글